长方体的体积教学设计
体积,几何学专业术语,是物件占有多少空间的量。体积的国际单位制是立方米。下面给大家分享长方体的体积的教学设计,欢迎借鉴!

《长方体的体积》教学设计
教学目标:
1、让在观察、比较中,感知长方体的体积大小与它的长、宽、高有关。通过具体操作,探索并掌握长方体、正方体体积的计算方法,能正确计算长方体、正方体的体积,并能运用所学知识解决一些实际问题。
2、在观察、操作、探索的过程中,提高学生动手操作及合作学习能力,培养迁移、类推能力和抽象概括能力,进一步发展学生的空间观念。
3、在个人及小组的探究活动中,培养团队协作,勇于探索的品质,体会数学的应用价值。
教学重点:引导学生探索长方体体积的计算方法。
教学难点:体验公式的推导过程。
教学过程:
一、复习比较,引入课题
1、(出示两个不同的物体)这两个物体谁比较大?我们比的是他们的什么?体积指的是什么?
2、下面的图形都是由棱长为1厘米的小正方体拼成的,它们的体积各是多少?你是怎么知道的?
3、(出示包装盒)大家认识它吧?它是什么形状的?
它的体积多大呢?请你估一估,猜猜它有多大?(生猜测,附带体积单位。)
要使他说得更准确,我们得来计算长方体的体积。这节课我们就来研究这个问题吧,板书课题:长方体的体积。
二、自主学习,合作探究
(一)探究长方体的体积计算
1、探究长方体的体积和那些因素有关。
师:我们都知道长方体有六个面,这6个面可能是什么形?
学生口答。
大家想一下,长方形的面积和什么有关?(学生回答)那么猜一猜,长方体的体积可能和什么有关呢?(生猜测)
老师这里有几组长方体,(课件出示)大家看,这两个长方体的长、宽、高有什么关系?
由此,我们可以得出什么结论?(长方体的体积与它的长、宽、高都有关系。)
2、探究长方体的体积和它的长、宽、高的关系,推导长方体体积的计算方法。
师:那么长方体的体积和它的长、宽、高到底有什么样的关系呢?接下来,让我们在实验中来研究一下。(每组准备12个小正方体)先来听一下实验要求。
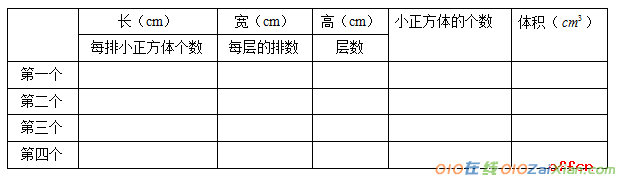
(1)摆一摆:四人一小组,用24个1立方厘米的正方体小木块,每人摆出一个长方体(尽可能不同)请组长给长方体编号(1)(2)(3)(4)
(2)看一看:每个长方体的长、宽、高分别是多少?记录它们的长、宽、高,填在表中。(给每组发一张课前准备好的如下表格)

(4)想一想:观察表中这些长方体的长、宽、高以及它们的体积,再联系数体积的过程,你发现了什么?在小组里谈一谈。
(5)汇报交流,发现总结长方体体积公式
师:观察表格,所用小正方体的个数和长方体的体积之间有什么关系?
生:我们组发现:长方体体积与数出的小木块的数量相等。
师板书:长方体体积=数出的小木块的数量
师问:再看看所用小正方体的个数与所拼接长方体的长、宽、高的关系。
生:所用小正方体的个数正好等于长乘宽乘高的积。
师:那么长方体的体积等于小正方体的个数,小正方体的个数正好是长×宽×高的积,你能总结长方体体积与长宽高的关系吗?
生:长方体的体积=长×宽×高
师板书:长方体的体积=长×宽×高
(6)课件演示公式的推导过程
如果用V表示体积,a表示长,b表示宽,h表示高,那么这个公式用字母怎样表示?
师板书:V=abh
(7)根据这个公式,要求长方体的体积,需要知道长方体的什么?
同生们学会了总结长方体体积的计算方法,真是了不起,通过猜想、实验、验证总结出了长方体的体积计算公式,今后在学习上同样可以利用这种方法学习。
3、长方体的体积计算公式的应用
(1)师问:那么课前的包装盒,怎样才能知道它的体积是多少呢?(全班动笔做一做。)
(2)师:同学们学习效率可真高,这么快就掌握了长方体体积的计算方法,那么,你们能帮冰柜司机解决这个问题吗?(课本练习43页)
三、知识延伸,拓展思维。
1、课件出示正方体。
师提问:这个图形是什么,有什么特征?你能结合刚刚长方体体积公式,想想如何计算正方体体积,与同学交流你的想法。
2、学生讨论后得出,师课件出示并板书:正方体的体积=棱长×棱长×棱长
用字母表示V=a×a×a=a3
强调:正方体是特殊的长方体
3、师介绍:a3读作“a的立方”
课件出示:一块正方体石料,棱长是6分米,这块石料的体积是多少立方分米?
学生独立完成,然后汇报交流。
四、巩固提高
1、有一本新华字典,它的长、宽、高分别是2分米、1分米、0.6分米.这本字典重多少千克?(每立方分米重500克)
2、一块砖的长是24厘米,宽是长的一半,厚是6厘米,它的体积是多少立方厘米?
五、全课小结,布置作业
1、通过这节课你学到了哪些知识?
2、布置作业
课外实践:找一个长方体实物量一量它的长、宽、高,并计算它的体积。
《长方体的体积》教学设计2
一、教学目标
【知识与技能】
知道长方体体积公式的`推导过程,掌握长方体体积的计算公式。
【过程与方法】
在观察、操作、探索的过程中,进一步发展空间观念,增强动手操作、抽象概括和归纳推理的能力。
【情感态度与价值观】
在合作探究的学习中,体验学习数学的乐趣,增强对数学的学习兴趣。
二、教学重难点
【重点】
长方体体积的计算方法。
【难点】
长方体体积公式的推导过程。
三、教学过程
(一)导入新课
1.复习回顾:物体的体积概念和单位。
2.用课件展示生活中常见的长方体,提问长方体的体积该如何计算。
(二)生成新知
1.操作转化
提问:长方体的体积与哪些数据有关?引导学生通过数组成几个不同形状的长方体的小正方体的个数记录、整理数据。
分组实验,教师巡视。
学生操作预设:学生数面前长方体时在数小立方体时和同组其他同学不同,教师可以引导学生按一定的顺序来数小正方体,从左往右依次数体积为1立方厘米的小正方体;学生在实验后对数据的记录不够工整,教师可以建议学生将所得数据参考教材中的方格进行填写。
学生汇报展示,总结发现:长方体的体积与长、宽、高有关。
2.操作探究,验证猜想
提问:用棱长1厘米的小正方体来摆一个长是5厘米,宽是4厘米,高是3厘米的长方体,它的体积是多少?
学生独立思考后汇报:长方体的体积等于长乘宽乘高。
3.总结概括
问题:你能写出长方体的体积公式吗?
总结并板书公式:长方体的体积=长×宽×高。

(三)巩固提高
1.课件展示不同长、宽、高的长方体,组织同学们计算各个长方体的体积。
2.展示两个具体的长方体,比较那个长方体的体积大小。
(四)小结作业
小结:师生共同总结本节课的收获。
作业:在生活中,找两个长方体并量出它们的长宽高,计算出它们的体积。
四、板书设计

【长方体的体积教学设计】相关文章:
本文来源:http://www.010zaixian.com/yuwen/jiaoxuesheji/2689505.htm