1,如图矩形ABCD对角线AC、BD交于O,E F分别是OA、OB的中点(1)求证△ADE≌△BCF:(2)若AD=4cm,AB=8cm,求CF的长。
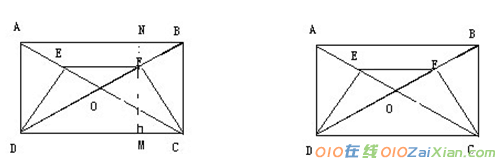
证明:(1)在矩形ABCD中,AC,BD为对角线,
∴AO=OD=OB=OC
∴∠DAO=∠ADO=∠CBO=∠BCO
∵E,F为OA,OB中点
∴AE=BF=1/2AO=1/2OB
∵AD=BC, ∠DAO=∠CBO,AE=BF
∴△ADE≌△BCF
(2)过F作MN⊥DC于M,交AB于N
∵AD=4cm,AB=8cm
∴BD=4根号5
∵BF:BD=NF:MN=1:4
∴NF=1,MF=3
∵EF为△AOB中位线
∴EF=1/2AB=4cm
∵四边形DCFE为等腰梯形
∴MC=2cm
∴FC=根号13cm。
2,如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=2DC,对角线AC⊥BD,垂足为F,过点F作EF∥AB,交AD于点E,CF=4cm。
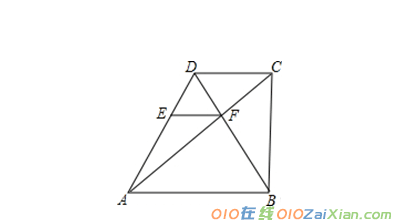
(1)求证:四边形ABFE是等腰梯形;
(2)求AE的长。
(1)证明:过点D作DM⊥AB,
∵DC∥AB,∠CBA=90°,
∴四边形BCDM为矩形.
∴DC=MB.
∵AB=2DC,
∴AM=MB=DC.
∵DM⊥AB,
∴AD=BD.
∴∠DAB=∠DBA.
∵EF∥AB,AE与BF交于点D,即AE与FB不平行,
∴四边形ABFE是等腰梯形.
(2)解:∵DC∥AB,
∴△DCF∽△BAF。
∴CD AB =CF AF =1 2。
∵CF=4cm,
∴AF=8cm。
∵AC⊥BD,∠ABC=90°,
在△ABF与△BCF中,
∵∠ABC=∠BFC=90°,
∴∠FAB+∠ABF=90°,
∵∠FBC+∠ABF=90°,
∴∠FAB=∠FBC,
∴△ABF∽△BCF,即BF CF =AF BF ,
∴BF2=CFAF.
∴BF=4 2 cm.
∴AE=BF=4 2 cm.
3,如图,用三个全等的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH,连接AE与BG、CF分别交于P、Q,
(1)若AB=6,求线段BP的长;
(2)观察图形,是否有三角形与△ACQ全等?并证明你的结论
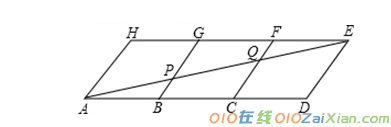
解:(1)∵菱形ABGH、BCFG、CDEF是全等菱形
∴BC=CD=DE=AB=6,BG∥DE
∴AD=3AB=3×6=18,∠ABG=∠D,∠APB=∠AED
∴△ABP∽△ADE
∴BP DE =AB AD∴BP=AB AD DE=6 18 ×6=2;
(2)
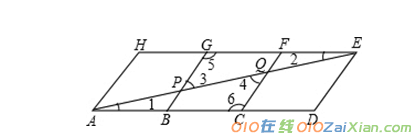
∵菱形ABGH、BCFG、CDEF是全等的菱形
∴AB=BC=EF=FG
∴AB+BC=EF+FG
∴AC=EG
∵AD∥HE
∴∠1=∠2
∵BG∥CF
∴∠3=∠4
∴△EGP≌△ACQ。
4,已知点E,F在三角形ABC的边AB所在的直线上,且AE=BF,FH//EG//AC,FH、EC分别交边BC所在的直线于点H,G
1 如果点E。F在边AB上,那么EG+FH=AC,请证明这个结论
2 如果点E在AB上,点F在AB的延长线上,那么线段EG,FH,AC的长度关系是什么?
3 如果点E在AB的反向延长线上,点F在AB的延长线上,那么线段EG,FH,AC的长度关系是什么?
4 请你就1,2,3的结论,选择一种情况给予证明
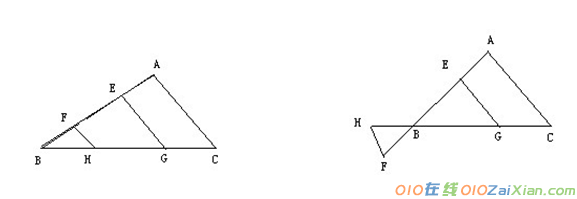
解:(1)∵FH∥EG∥AC,
∴∠BFH=∠BEG=∠A,△BFH∽△BEG∽△BAC.
∴BF/FH=BE/EG=BA/AC
∴BF+BE/FH+EG=BA/AC
又∵BF=EA,
∴EA+BE/FH+EG=AB/AC
∴AB/FH+EG=AB/AC.
∴AC=FH+EG.
(2)线段EG、FH、AC的`长度的关系为:EG+FH=AC.
证明(2):过点E作EP∥BC交AC于P,
∵EG∥AC,
∴四边形EPCG为平行四边形.
∴EG=PC.
∵HF∥EG∥AC,
∴∠F=∠A,∠FBH=∠ABC=∠AEP.
又∵AE=BF,
∴△BHF≌△EPA.
∴HF=AP.
∴AC=PC+AP=EG+HF.
即EG+FH=AC.
5,如图是一个常见铁夹的侧面示意图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA于点D,已知DA=15mm,DO=24mm,DC=10mm,我们知道铁夹的侧面是轴对称图形,请求出A、B两点间的距离。
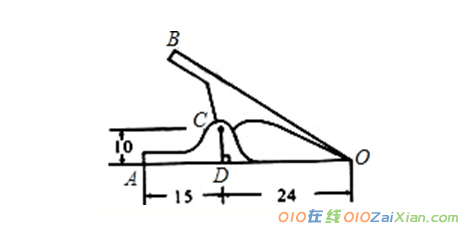
解:连接AB,同时连接OC并延长交AB于E,
因为夹子是轴对称图形,故OE是对称轴,
∴OE⊥AB,AE=BE,
∴Rt△OCD∽Rt△OAE,
∴OC:OA = CD:AE
∵OC=OD+CD ∴OC =26,∴AE= =15,∵AB=2AE ∴ AB =30(mm)。(8分)
答:AB两点间的距离为30mm。
【初二数学几何考试题】相关文章:
1.初二数学月考试题
2.数学几何小报图片
本文来源:https://www.010zaixian.com/shiti/2602691.htm